Mekkora szárny kell egy tündérnek, hogy repülhessen?
Itt a farsang, jelmezekben szaladgálnak gyerekek, felnőttek. Sok farsangi jelmezen látok szárnyakat. Kislányok között népszerű a pillangó és a tündér, fiúk talán gyakrabban öltöznek pilótának, vagy Batmannek. Valahogy gyerekkorunk óta él bennünk a vágy, hogy repülni tudjunk, messzire eljussunk, akadályok nélkül közlekedjünk és mindent átlássunk felülről.

(Designed by user2104819 / Freepik)
Magam is végig néztem jó pár Barbie-rajzfilmet a gyerekeimmel, ahol pillangó-szárnyakon könnyedén suhantak a levegőben a rózsaszín szereplők. Technikai képzettségű ember lévén nem tudtam szó nélkül hagyni a látottakat és a film után beszéltünk lányommal arról, hogy egy ilyen szárny fel tud-e emelni valakit. Nem, nem romboltam le teljesen az illúziót, csak kontextusba helyeztem, valahogy így:
„Ahhoz, hogy egy szárny felemeljen valakit, kell egy bizonyos sebesség egy jókora ügyesen kidolgozott szárny-felület, ami nem csukódik össze a terhelés alatt”.
A sebesség azért kell, mert a szárny felhajtóereje a dinamikus nyomással arányos (Pdyn), ami nem más, mint az a nyomás, ami a levegő mozgási energiájából, vagyis sűrűségéből és sebességéből származik és így számolható:
Pdyn= airspeed2*density/2
Ezt kell megszorozni a szárny felületével és egy a szárny geometriájára és állásszögére jellemző felhajtó erő tényezővel (ez maximálisan picit 1 felett van egy jól megtervezett szárnyra).
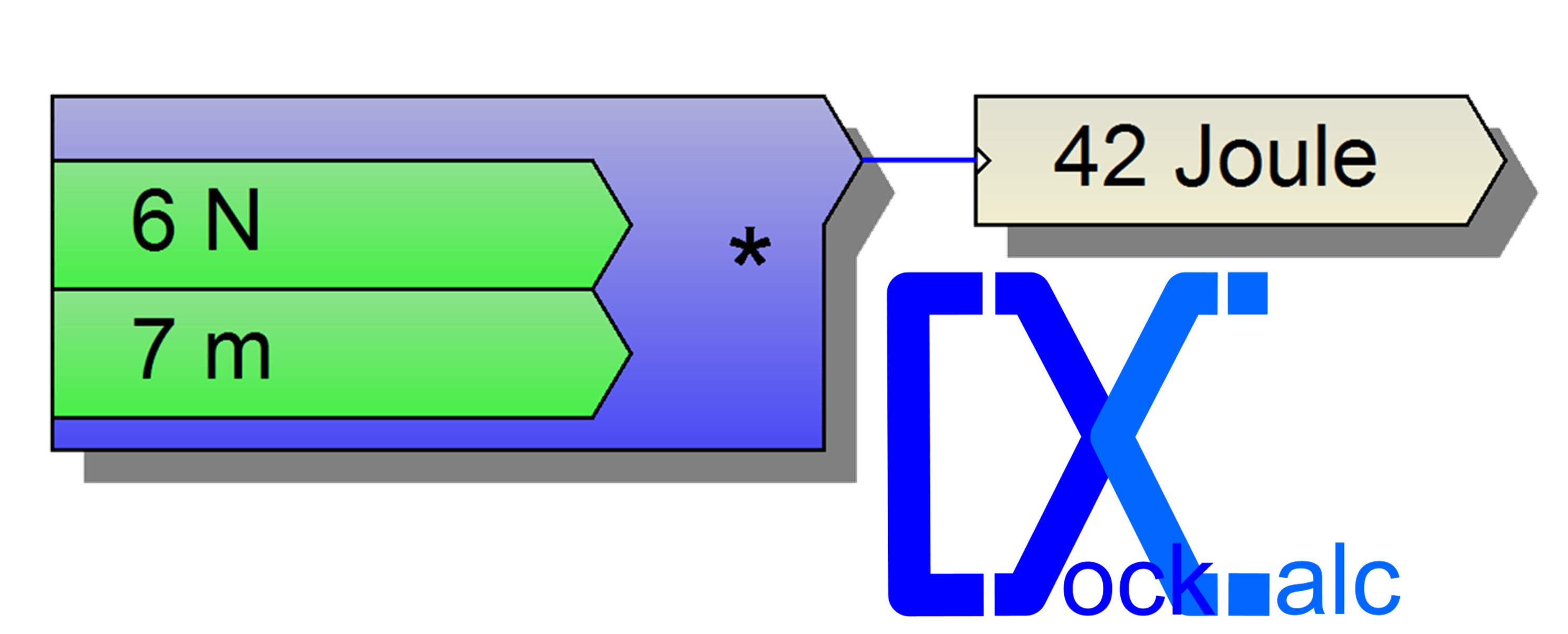
Flift=Awing*Clift*Pdyn
vagyis
Flift=Awing*Clift* airspeed2*density/2
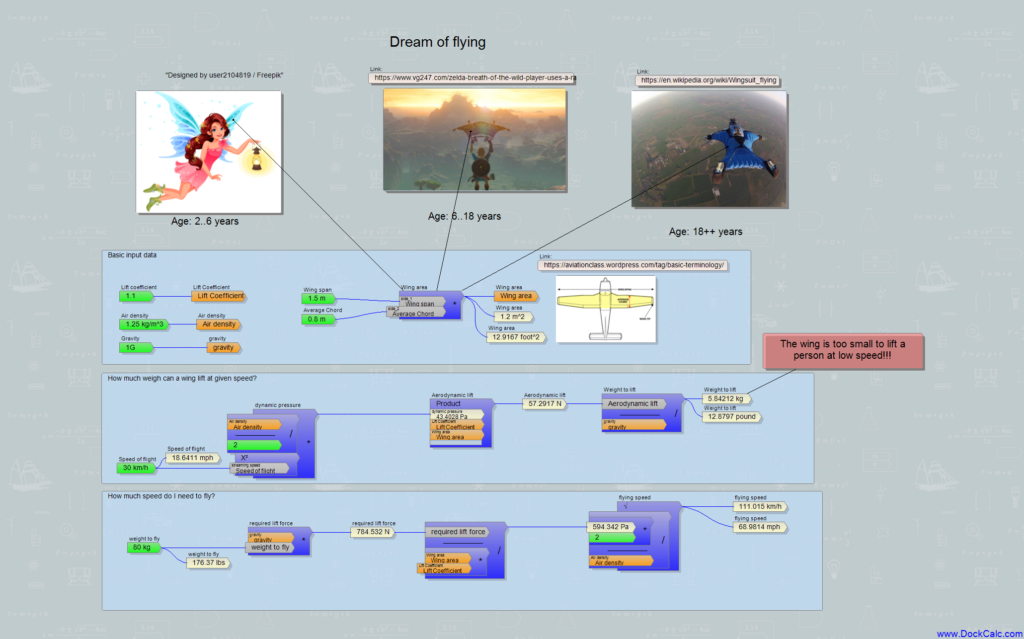
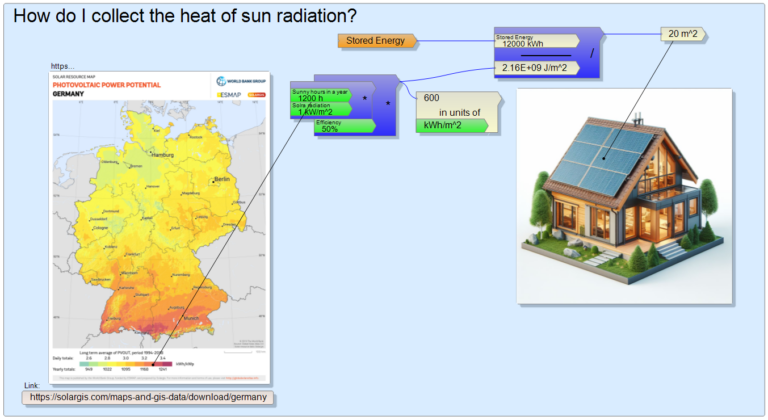
Aki nem szeret ilyesmit számolni, vagy fél, hogy belebonyolódik a mértékegységekbe, az ne búsuljon, neki való a DockCalc program, ezzel számolgattam én is, mégpedig azt a súlyt (pontosabban tömeget), amit egy szárny adott sebességnél meg tud még emelni, és ugyanezt visszafelé is, tehát hogy mennyi sebesség kellene egy adott felületű szárnynak ahhoz, hogy egy adott tömegű testet (tündér, Batman, Red Bull-influenszer, repülőgép,…) felemeljen. Így néz ki a számítás grafikusan:
Aki mégis számológéppel és papírral állna neki, annak figyelni kell a mértékegységek helyes használatára. Ha a sebességet km/órában írod be a képletekbe, akkor az eredmény mértékegysége nem lesz barátságos, tehát a képletben célszerű mindent az SI mértékegységekben kezelni (m/s, kg, N, Pa) és akkor az eredmény is ilyen mértékegységekben adódik.
Akik az angol/amerikai hagyományos mértékegységekkel érzik magukat otthon, azok nagyobb papírt készítsenek elő, mert, ha csomóban írják be a sebességet, font/köblábban a sűrűséget, majd Psi-ben (font per nényzet-incs 😊) szeretnék látni a nyomást, azoknak lépten nyomon át kell váltani a részeredményeket.
Visszatérve a repülés vágyához – mit is lehet tanulni a képletekből?
- minél gyorsabban repül valami, annál kisebb szárny kell
- minél könnyebb valami, annál kisebb szárny is elég
A kritikus szituáció a le és felszállás, hiszen ekkor a sebesség nem olyan nagy, mint utazás közben. Egy tündér esetében szerencsére kicsi a súly, de így sem árt, ha gyorsan tud futni: egy 40 kilós rövidtávfutó tündér egy rajzfilmbe illő pici szárnyacskával (~1.5 m2) jó 70 km/h-val kellene nekifusson, hogy elemelkedhessen. Csak egy jóval nagyobb szárny segít, ami viszont már nem olyan elegáns és nehéz vele beülni egy cukrászdába.
Ha felszállást inkább egy korty Red Bull kíséretében valahonnan leugrással helyettesítjük, akkor egy 80 kilós adrenalin-függő speciális denevér-szerű ruhában (WingSuit) akár valamivel 100 km/h felett már képes repülni. Itt azért megjegyzem, hogy a repülés és zuhanás közötti átmenetről van szó, hiszen 100 km/h-s repüléshez nagyjából 40 km/h zuhanási sebesség tartozik, neki ejtőernyőt kell nyitni földet érés elött! Nehogy anélkül próbálkozzon valaki!
Aki tartósan fenn akar maradni szárnyakkal, annak hajtania kell magát valahogy. Erre sok lehetőség van, a legismertebbek ezek:
- csapkodó szárny
- motor és légcsavar
- gázturbina
- rakétahajtómű
- felszálló légáramlat
Mindezek ellenére nem akarok elszomorítani senkit azzal, hogy nem tud otthon a garázsban saját repülő eszközt építeni. Találtam a YouTube-on egy srácot, aki szó szerint barkács eszközökkel dolgozva nem is egy ultrakönnyű repülőgépeket épít és veszi a bátorságot, hogy felemelkedjen vele. Volt néhány pillanat, amikor alig hittem a szememnek, nem értettem, hogy mi adja a srác bátorságát egy hanyagul ragasztott Hungarocell-szárnyra bízni az életét, de végül a szerkezet kibírta a repülést.
Ha tehát kell egy kis inspiráció saját repülőgéped építéséhez, akkor nézd meg ezt a linket!
Ajánlom a gép tervezéséhez a DockCalc programot, de ha leesel, nem vállalom a felelősséget!
A fenti számítási file-t letöltheted itt: