A Porcukor felülete

Ahogy közeledik a karácsony, előkerülnek a finomabbnál finomabb sütemény-receptek, ünnepi süti-illat tölti be az otthonokat. Természetesen a sütik tetején nem hiányozhat a vékony porcukor réteg, amely talán egy picit a havas téli tájat is szimbolizálja. Amikor esszük, szinte elolvad a szánkban, nem úgy, mint a nagy szemű kristálycukor, ami serceg a fogaink között, amikor rágunk. De miért is olyan finom a porcukor, mi a titka, ami a kristálycukorból hiányzik? Ha mérnökként tekintem, akkor az az ötletem, hogy nem kell tovább rágni, mert már finom szemű és hogy nagy a felülete, ezért hamar feloldódik. Ha porcukrot teszek a teámba, sokkal hamarabb feloldódik, mint a kristálycukor. Ha pedig egy szállodában véletlenül csak nagy szemcsék formájában találok cukrot, jó negyedóráig kell várnom, míg eltűnik és végre ihatom a teámat. Ha tehát a felület olyan fontos, vajon mekkora a felülete a porcukornak? Egy gondolatkisérlettel be lehet látni, hogy minél kisebb a szemcséje, annál nagyobb felület válik szabaddá az oldódás számára:

Gondoljunk csak bele, ha lenne egy olyan nagy cukorkristályunk, mint egy Rubik-kocka, annak csak a külső felülete szabad, ott tud hozzáférni bármilyen ital, amit avval akarnánk megédesíteni. El is tartana jó darabig, mire feloldódna. Ha felosztanám a nagy kockát úgy, hogy minden irányban elfelezném, kapnék összesen 8 fele akkor kockácskát. A vágási síkok mindkét oldala, mint új külső felület válna szabaddá. Ha az eredeti kocka éle „a” volt- akkor keletkezik 3 új vágási síkom (egy vízszintes és két egymásra merőleges függőleges), melyek mentén 3*2 darab „a*a” felületet nyertem. A 2-es szorzó arra utal, hogy a vágási sík mindkét oldala számít. Ha valakinek a fantáziája gyakorlati tapasztalatot is igényel, ajánlom a gyakorlatot például sajttal végrehajtani.

Ha az eredeti kocka éle „a” volt, akkor annak a felülete 6*a². A felhasítás útján 3*2*a² felület jött hozzá, ami azt jelenti, hogy megdupláztam a kocka felületét. Ez úgy is belátható, hogy a 8 darab a/2 élhosszú kocka összes felülete: 8(darab)*(a/2)²*6 = 8*a²/4*6 = 12*a².

Ha a kisebb kockákat újra elfelezem ugyanígy 3 sík mentén, ismét új felületek jelennek meg.

Szóval, ha oldalfelezéssel 8 kisebb kockára hasítok egy kockát, megduplázódik a felülete. Ha a hasításokat egy darálóra bízom és rengeteg picike kockát (cukorszemcsét) csinálok egy nagyobb tömbből, minél apróbbra darálom, annál nagyobb lesz az összes felület.

Vajon nagyjából mennyi felülete van egy 500g-os csomag porcukornak összesen?

Ha gonosz matematika-tanár lennék, kézzel végigszámoltatnám a tanulókkal, hogy mondjuk 10-15 felezéssel mennyi felület jönne ki. Gonosz matektanár helyett inkább lusta mérnök vagyok, ezért a következő gondolatmenettel dolgozom:

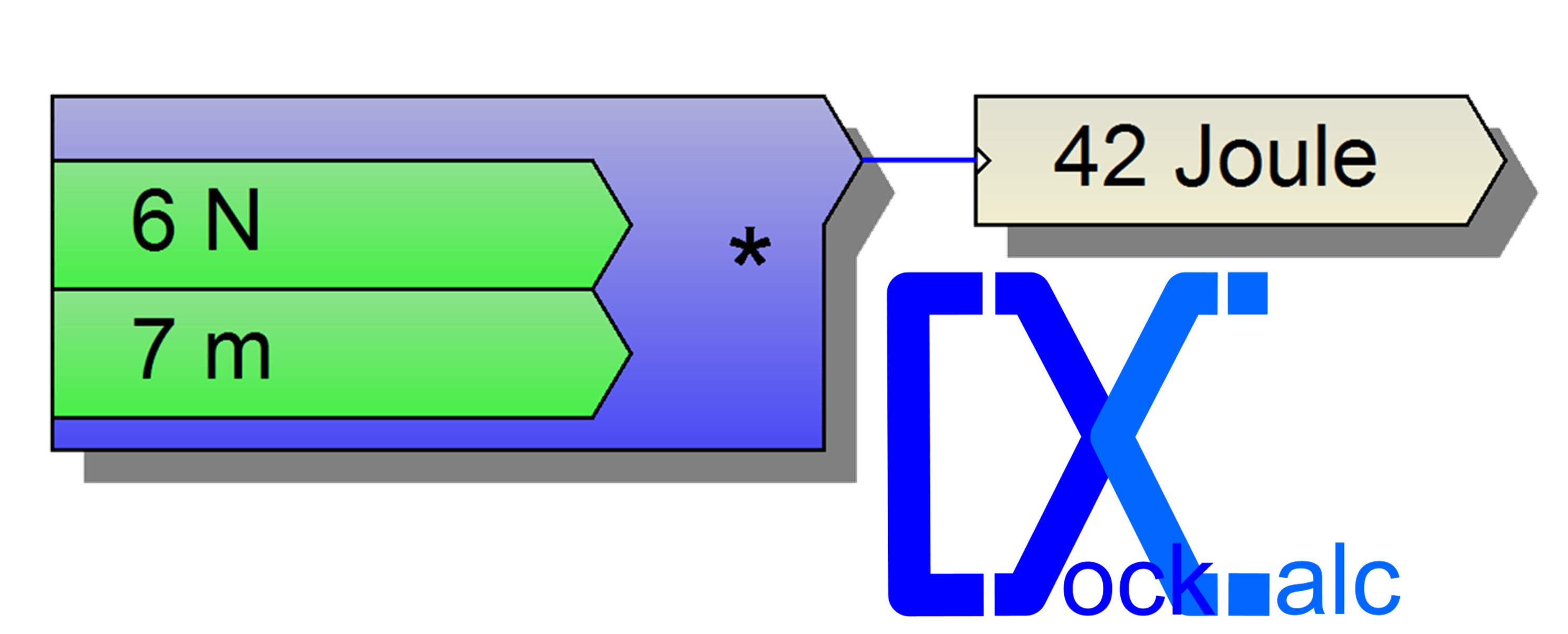
1: felírom egy adott méretű kocka felületének és térfogatának a hányadosát: Felület=6*a², Térfogat=a³. Felület/Térfogat=6*a²/a³=6/a. Az „a” -val való osztás mutatja sejtésünket: minél kisebb az „a” (szemcseméret), annál nagyobb az arány a felület javára és még mértékegysége is lesz az aránynak: [1/m]. Az „a” méretre az interneten 0.02mm és 0.1 közötti értékeket találtam.

2: kiszámolom egy 500g-os cukortömb térfogatát (csak a cukor sűrűséget kell google-nem hozzá, számtalan forrás szerint nagyjából 1600 kg/m³). 0.5kg/(1600 kg/m³) = 0.0003125m³ (vagyis 0.3125 Liter).

3: A fenti két adat birtokában bármilyen „a” szemcseméretre ki tudom számolni az egész doboz cukor összes felületét:

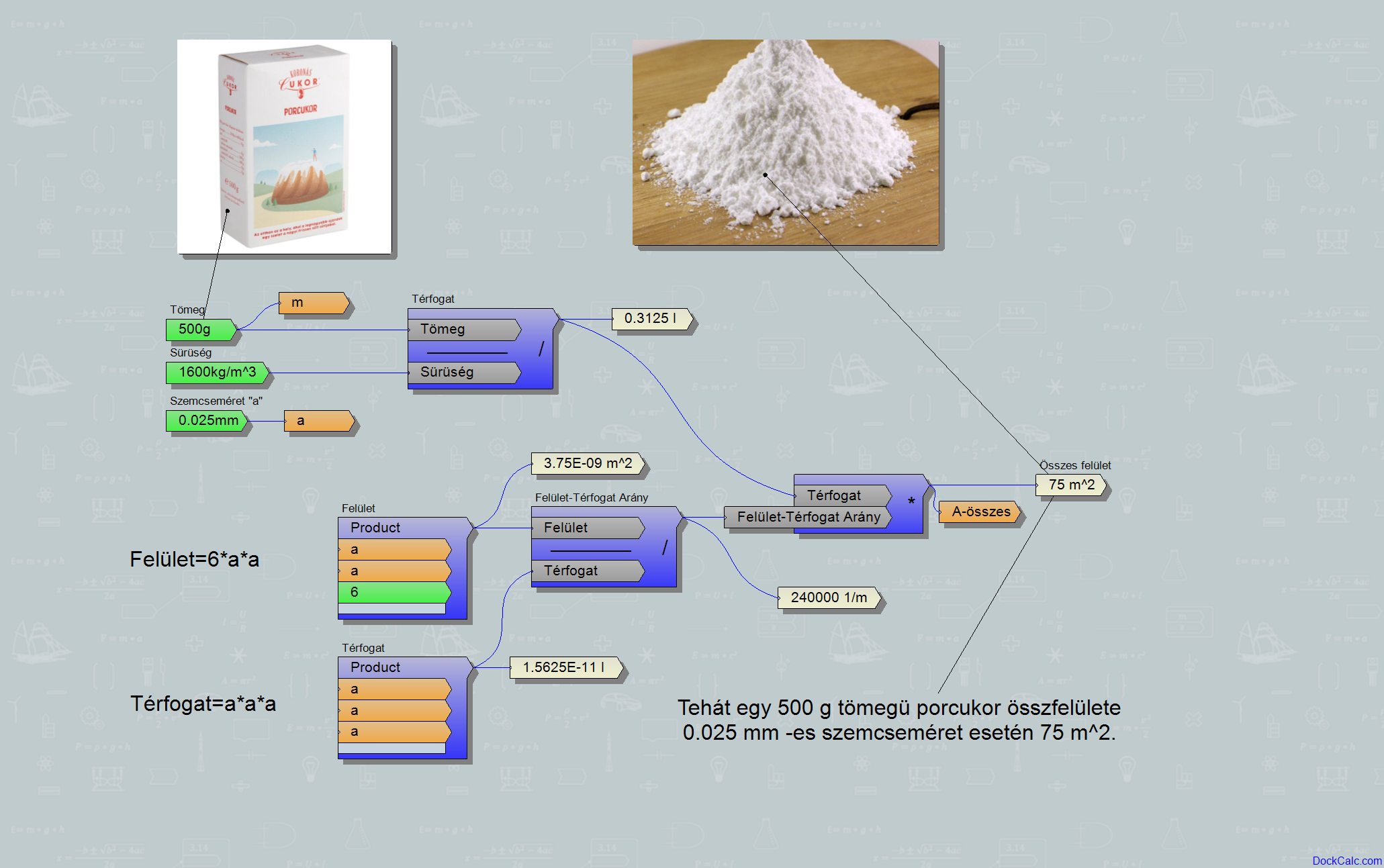
Összfelület=Térfogat*(Felület-Térfogat arány). Nekem nagyjából egy lakás alapterületének megfelelő felület (75m²) jön ki 500g porcukorra.

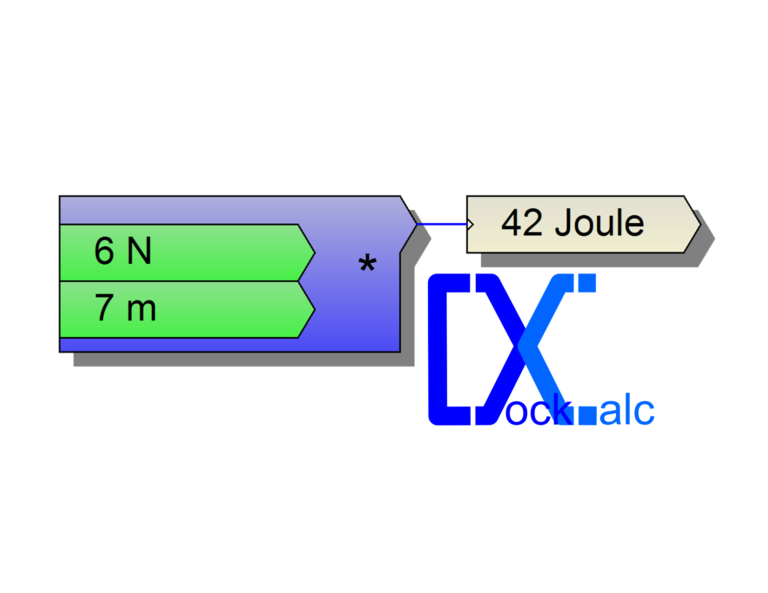
A DockCalc programmal összeállítottam egy ilyen számítást, így mindenféle adatkombinációra gyorsan kapok eredményt:

A fenti számításban persze egyszerűsítések vannak, például, hogy a cukor bármilyen kis szemcséjű, azért kocka formájú. Érdekes módon például a só mikroszkópos képe tényleg elég kocka formájú. Ha a valóságban a formák eltérnek, attól még az eredmény nagyságrendje nem tér el durván. Ennél sokkal érdekesebbnek tartom viszont azt az általános érvényű összefüggést, miszerint, ha valamilyen formát kicsinyítek vagy nagyítok a felületének és térfogatának aránya a méret csökkenésével növekszik.

Számtalan helyen tapasztalható ez a hatás, álljon itt néhány példa:

• A nagy csepp-méretű esőcseppek gyorsabban zuhannak, mint a finom szemcséjű eső (felületük fékezi őket, térfogatukból adódó súlyuk pedig hajtja). Ha cseppek mérete elég kicsi (pl. köd, felhő), akkor olyan lassan zuhannak, hogy a legkisebb felfelé áramló fuvallat is megállítja vagy akár felemeli őket.
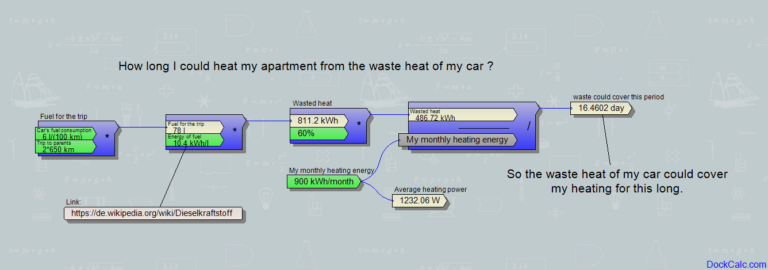
• Motorokban az üzemanyag elégetéséhez fontos a nagy felület, ezért próbálják a mérnökök minél kisebb cseppekre porlasztani az üzemanyagot. Ehhez kapcsolódik egy híres magyar találmány, a Bánki-Csonka porlasztó (Link) és ezért igyekeznek a mai Diesel motorokban is növelni a befecskendezési nyomást (2000 szeres légköri nyomás fölé), hogy az apró lyukakon a legkisebb szemcseméretre porladjon. Minél jobban sikerül, annál inkább hozzáfér az oxigén égéskor a cseppekhez, így annál kevesebb káros korom keletkezik.
• Az élőlények testsúlya a méretük 3-ik hatványával arányos, csontjainak keresztmetszete viszont csak a méret négyzetével. Minél nagyobb egy élőlény, annál nagyobb a csontjára és izmaira ható terhelés. Létezhettek olyan nagy testű dinoszauruszok, amelyekről úgy gondolják tudósok, hogy csak vízben tudtak normálisan létezni, mert lábaik a szárazföldön nem bírták volna el súlyukat. Másfelől kisebb állatok, rovarok egész nagy magasságból való zuhanást túlélnek sérülés nélkül. Részben a légellenállás, részben a lábak fajlagos terhelése az ok, mindkettőben a felület és térfogat aránya a kulcs.

Na de inkább térjünk vissza a süteményekhez: Jó étvágyat és vigyázzunk a porcukorral: már egy négyzetméter is hizlal 😊!