How many square millimeters is your car’s fuel consumption?
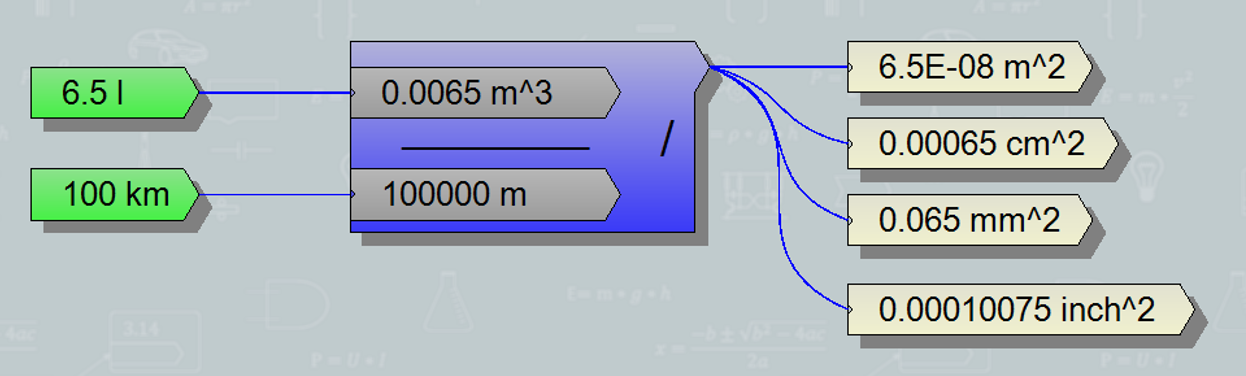
It’s a very strange question, I know, but I can explain it: My car has an average of 6.5 l/100km fuel consumption. When I typed this into my DockCalc program, the program immediately converted it to square meters (this is the strength of the software, that it understands the units of measure and helps to calculate with them). At first, I suspected a calculation error, but then I realized that the machine was not mistaken:
If I simply divide 6.5 liters by 100 km, the way I divide two physical quantities in a high school physics class, I get a numerical value and a surface unit.
For example like this:
This is surprising at first, but understandable, since by dividing volume by length, I should get a surface or cross-section. In the case of my car, it was 0.065 mm2.
Fantasy was needed so that I could assign this cross-section to some “real” meaning. And I have a good fantasy: I imagined my car sucking up a very long straw filled with fuel lying on the side of the road, or rather holey pasta (the thin Italian pasta with hole is called Bucatini). If the internal cross-section of this “diesel-Bucatini” is exactly 0.065 mm2 (~0.28 mm diameter!), then the engine receives exactly as much fuel from the dough-pipe during driving as it consumes on average. I elegantly neglect the nutritional value of the dough, because the engine can’t do anything with it.
If the pasta-eating car doesn’t paint a dream-like picture, I recommend that you generate it with some artificial intelligence algorithm (like Midjourney):
I was actually surprised that a car is happy with so little, I thought I’d look at other vehicles as well:
An airplane is very impressive, it has enormous performance, although it also goes faster. What kind of consumption comes out of this?
Let’s look at an example: Airbus A350-1000 long-range passenger aircraft. You only have to fly with them once a year to destroy your ecological footprint. Roughly typical data on its consumption:
15,000 pounds/hour consumption at a speed of 492 knots (huh, I would not like to calculate this by hand). If I consider the 0.8 kg/l density of kerosene, the program calculates a consumption of 932.6 l/100 km.
Finally, some impressive value. Converted to a cross section as I did for the car: 9.32 mm2, which corresponds to a 3.4 mm diameter “straw”. So, if an airplane were to swallow a kerosene-filled straw about the thickness of that in McDonalds, both of its engines would be fueled perfectly. 932.6 l/100km sounded more frightening, although it is not that much when I look at the fact that it is less than 2.6 l/100km for each of the 369 seats (consumption per passenger). So if there are two people traveling in a car, a passenger plane would still be more fuel-efficient to transport them.
If I didn’t manage to calculate astonishing data even with an airplane weighing hundreds of tons, then let’s look at something even more brutal:
If there’s one thing on earth to consume a lot of fuel, it’s the SpaceX Falcon Heavy rocket. I confess that the peak of my technical experiences as an adult was the moment when, as I watched on YouTube, the two booster stages of the said rocket turned around in space after completing their work, and then, as if it were completely natural, they came back to earth and landed next to each other with the elegance of a ballet dancer. In that brief moment, I would have gladly exchanged with the members of the development team so that I could experience this feeling of success personally.
Well, now I would like to discuss the consumption of the vehicle:
All I know is that together with the boosters, they burned 3×123 tons of RP-1 (rocket grade kerosene) and about twice as much liquid oxygen. While this first stage was driving the vehicle, it was moved about 60km away from the ground. I don’t know how much lateral distance was included in the 60 km height, so I’ll generously take double it, 120 km as distance travelled.
Now is the time for the experts: who can tell how far the Falcon Heavy traveled before the first stage was cut off? I welcome answers in the comments section on any social media channel.
The other extremely generous thing I will do is that I don’t even include oxygen in the consumption, believe me, the data will still be amazing anyway! (if I counted it, the result would be three times as large.)
So, dividing 3×123 tons again by 0.8 kg/liter and by 120 kilometers, the consumption comes out to be 384375 l/100km. The straw equivalent, which was tiny 0.28 mm for the car, can now be compared to a 70 mm fire hose.
I can say with confidence that since the human race discovered fire-making, it has been cultivating it more and more intensively, and the peak of this is the launch of such a rocket. But if our species were to make the earth uninhabitable one day – for example by launching many of these rockets – then the comfort remains that the richest among us can transfer this knowledge to another planet – or at least the need to make a profit.
With this reassuring knowledge, I will also take now a sip of red wine. If I do this sitting in one place, i.e. while covering zero distance, then my specific consumption value even exceeds that of the Falcon Heavy, since dividing by zero will give an infinitely large result per 100km 😊.
As usual, here is an overview of the DockCalc calculation:





Akos, you are brilliant once again.
I devoured your article in one piece (with an equivalent diameter of more than 0.28mm²).
Your red wine punchline then puts the crown on the whole thing 🙂
Engineer’s greetings, Raphael
Hi Raphael, thanks a lot for the feed-back, it motivates me for next articles!
Best Wishes,
Ákos