Can I store summer sunshine to heat my house in winter?
After the long, warm summer came the cold, the morning temperature suddenly dropped to around freezing point. I’ve had plenty of sunshine for months, and now I’m suddenly really missing it. Today, my attention is focused on heating energy and as an engineer, my mind is already thinking about whether I could use some thermal storage to store excess heat in the summer for the winter so that I don’t have to pay for the heating energy anymore. After all, there are heat storage heaters that can store a day’s worth of heat and fit in a room, so you just have to make it “slightly” bigger. The plan would be to collect the heat of the summer sunshine, heat up some material with it, and then take out its heat slowly during the winter. I just need to clarify a few questions to see if the idea is feasible:
-how much energy are we talking about storing at all?
-how much solar surface do I need to collect the heat in summer?
-what kind and how much material can store the given amount of heat?
-how can I thermally insulate my storage so that the collected energy does not escape for months?
The article wouldn’t even be on this website if I didn’t use the DockCalc software for the above calculations, since I will need all kinds of units of measure, which the software simplifies for me. First of all, I want to know how much energy is needed for heating in a year. Fortunately, there are empirical values on the Internet that approximate the energy requirements of one square meter of different apartments. In the case of new apartments, the expectation is much less than 100 kWh/m2/year, but not all apartments are so modern, so I used 120 kWh/m2/year as a basis. I like round numbers, so I calculate with a 100 m2 apartment. The multiplication is simple, it can already be seen that I have to store heat energy of the order of 12,000 kWh.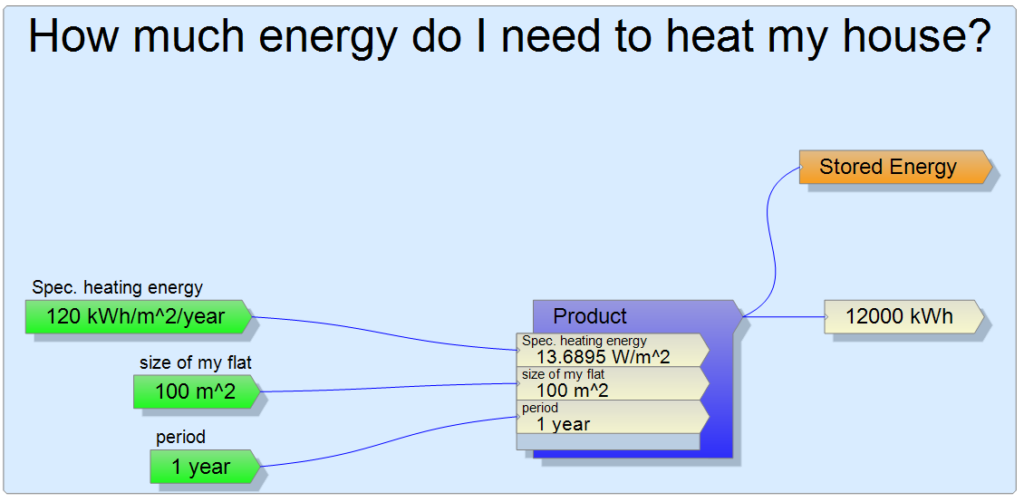
By the way, this is roughly equivalent to burning 1,000 liters of oil! Saving so much expensive and environmentally polluting oil is certainly a nice task.
Now let’s see how large solar surface I would have to install to collect the sun’s rays in order to have this amount of thermal energy during the year. For this, of course, I had to find data on the amount of annual sunshine, for example here:
https://solargis.com/maps-and-gis-data/download/germany
I live in Bavaria, so the situation is more fortunate than further north, based on the map, I can count on 1200 sunny hours in a year. Actually, the data of the map are given in kWh/kWp, i.e. kilowatt hour per kilowatt nominal peak power, specifically for solar cells producing electrical power. I consider this somewhat loosely as the average annual equivalent number of sunny hours. I believe that solar heat collectors are much more efficient than electric solar panels in the summer, so I took 50% of the total solar energy to be recoverable (compared to the modest 20% efficiency of electric solar panels). If I divide the 12,000 kWh by the 1,200 sunny hours and the well-known maximum of solar radiation of 1 kW/m2, I get a collector surface of 20 m2 with an efficiency of 50%: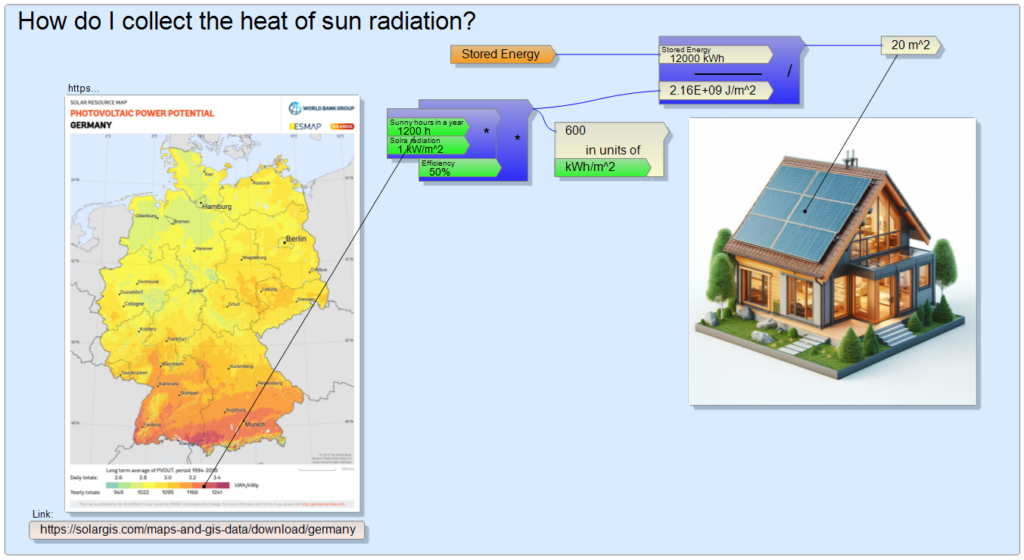
It might be worth it if I never had to pay for heating anymore.
I will now turn to the issue of heat storage. I don’t have to search much in heat capacity tables to see: I want to store the heat in the form of hot water.
Why? Because water is available in large quantities and is affordable, the solar collector is designed for this and has a world champion high heat capacity of 4200J/kg/K. It is no coincidence that water is revered as an ancient element, since it is the basis of life, a fantastic material, so we should appreciate it much more than we do.
By the way, I would like to note: the heat capacity of water is the definition of our caloric unit: one calorie (cal) is the heat energy required to heat one gram of water by one degree Celsius. Food packagings specify a thousand times this, the kilocalorie (kcal) for 100g food.
I have to make some assumptions about my imaginary heat storage:
– I think that by the end of summer I will heat the water in my thermal storage to 95 degrees Celsius.
– I would like it to be 65 degrees Celsius by the end of winter, so that the heating can work effectively with it.
Working with these data, I divide the 12000 kWh by a temperature difference of 30 Celsius and then by the heat capacity of the water (4200J/kg/K).
The resulting 342 tons makes me frown a bit, but I divide it by the density of water of 1000 kg/m3 to get the shocking volume of roughly 342 m3 in front of me.
I try to imagine this volume as a 2 meters deep circular pool, but unfortunately it turns out to have almost 15 m diameter, which is more suitable for the garden of a luxury hotel, not for the backyard of an average person who wants to save money on heating.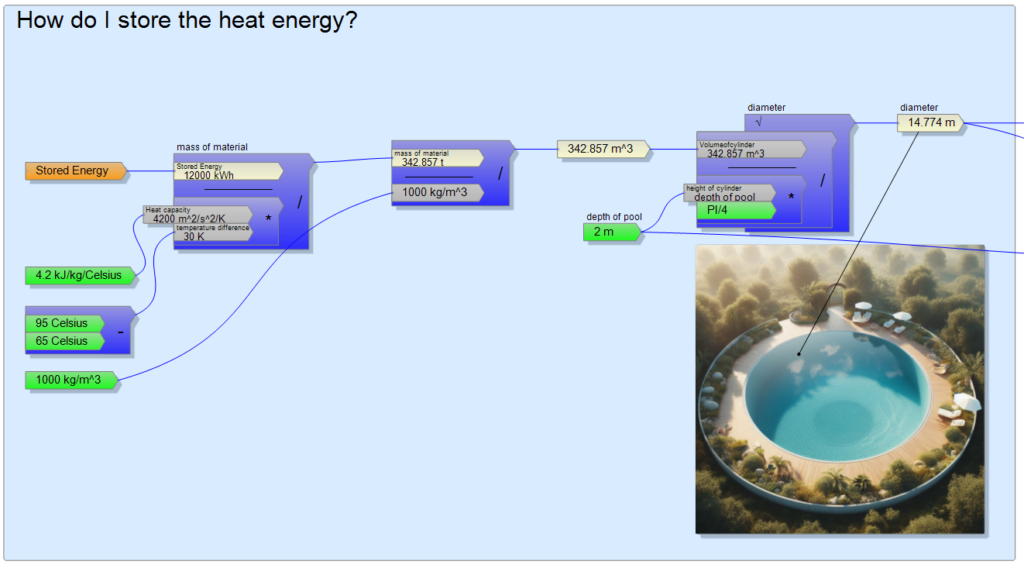
The bargaining of the disillusioned dreamer is going on in my head and he argues that you can definitely count on the late autumn and early spring sun rays so that you don’t need such a big pool, but I still can’t believe anything smaller than 10 meters in diameter. My initial enthusiasm is already a thing of the past, even though I didn’t even think about thermal insulation. Although the formula collection function of the DockCalc software helps to easily calculate the surface of the pool, 435 m2 makes you feel that the solution of isolation will not be easy. If I don’t want to allow more heat loss than 5% of the total stored heat (600 kWh) for half a year, the entire pool cannot emit more than 136 W of heat loss, which means 0.314 W/m2. Whether or not this can be solved depends on how effective my insulation is. The thermal conduction value of the popular Styropor panels (called Hungarocell in Hungary) is 0.035 W/m/K, which can also be understood as allowing 0.035 W of heat to escape per degree and per square meter at a thickness of 1 meter. However, there will be a difference of at least 70 degrees Celsius between my hot water storage and the winter weather outside, which means that 1 meter of thermal insulation already allows 2.45 W per square meter, even though the permissible value was 0.314. The bitter truth can be guessed from the ratio of the two numbers. My pool would need about 7 meters thick thermal insulation all around so that the energy cannot escape before it is used.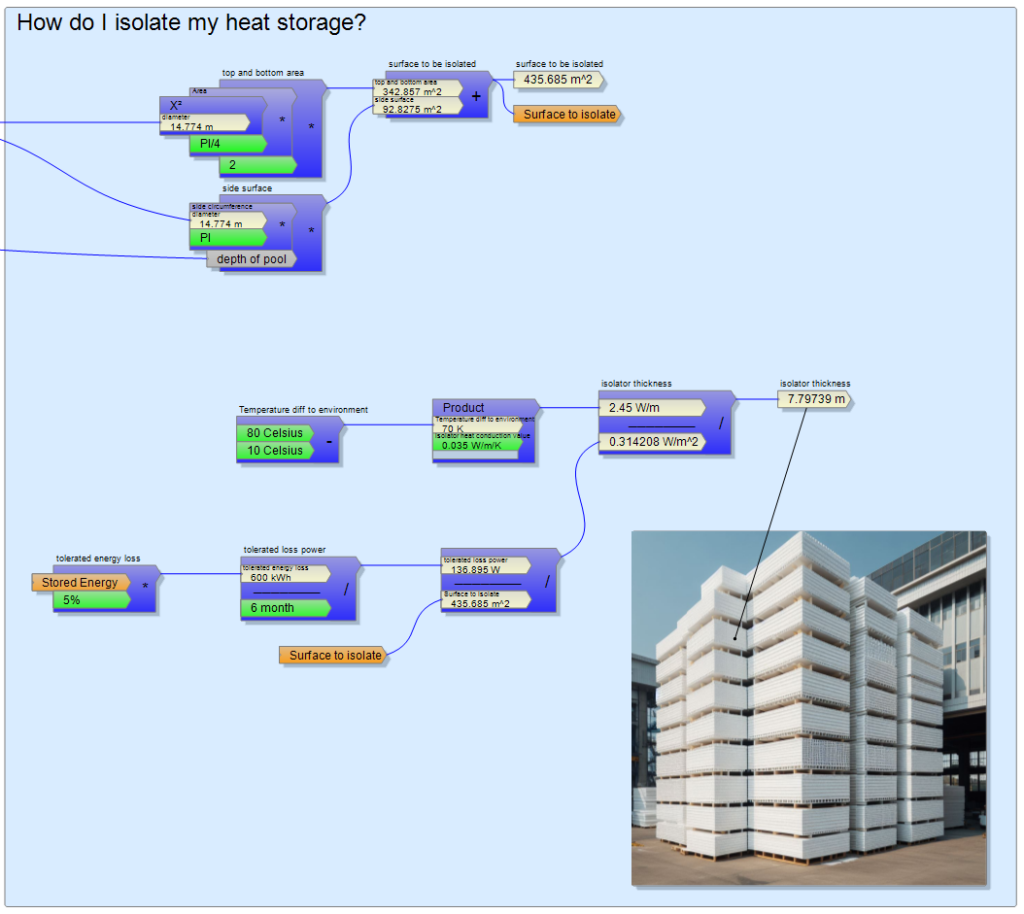
To put it mildly, something like this cannot be solved, unfortunately I have to wake up from my dream.
As good as it sounded that a collector with a completely realistic surface was enough to collect the sun’s heat, the amount of water required and the impossibility of insulation are so disappointing. If it were not so, surely many houses could get winter heat this way and we could save a lot of environmental pollution by such heat storage systems. It is true that using a smaller energy storage can also save a lot of heating energy. Fortunately, the weather is so versatile that there are also sunny phases during the heating season, so not all the energy needs to be “brought from the summer”, so the required heat storage can be much smaller than my very pessimistic calculation above.
If you set a less ambitious goal and only want a solar heater for summer showers, or use a solar collector only for supporting heating, feel free to calculate how big the collector you need and how much water and how much energy it shall store. For all such calculations, I kindly recommend the DockCalc software. Since I have programmed it, I will not start such estimations with anything else. If you like it, you can download it here. Have fun!
You find the above calculation file here:
DockCalc calculation file about how to collect and store the solar energy in summer to heat a house in winter.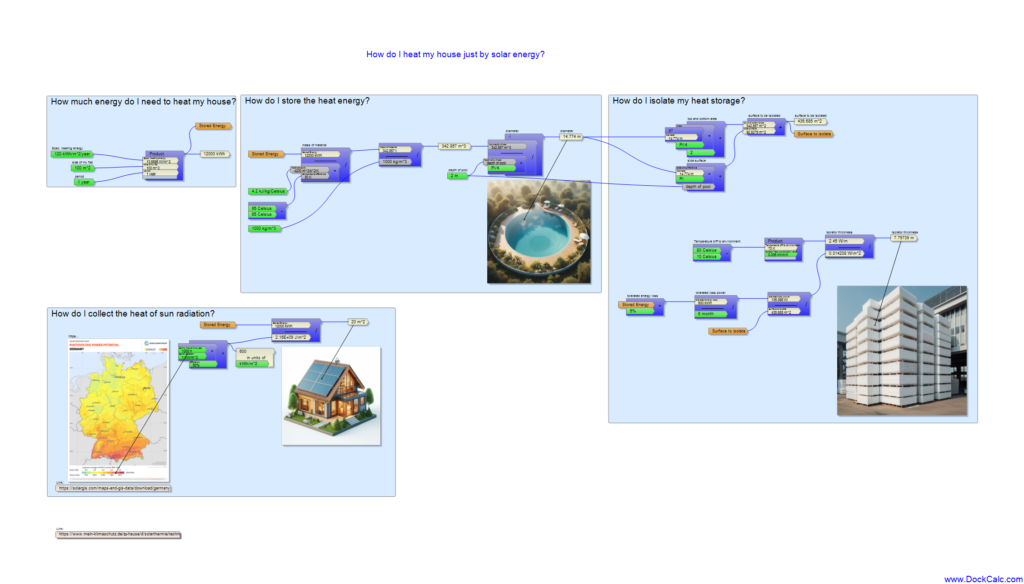 You need DockCalc application (DockCalc.exe) to open and edit this data file!
You need DockCalc application (DockCalc.exe) to open and edit this data file!