Bicycle gears and air drag calculation
One of the most brilliant inventions of mankind is the bicycle. It uses muscle power in a very efficient way to move forward, it is much faster than walking, it is healthy, and even some load can be carried. I can’t wait to ride my bike in the spring sunshine. This passion of mine goes back to my childhood, when I used to ride my bike a lot and, being a child with technical interests, I was always thinking about some kind of technical modification. Once, we replaced the rear wheel of my bicycle with a much smaller wheel of a children’s bicycle and enjoyed how easily it was possible to go uphill with it due to the changed wheel radius. How nice it would have been if I could have always chosen the wheel for each street slope separately. This desire of mine was later fulfilled by the bicycle with gears. Yes, children of today, at that time (I’m talking about before 1980) children’s bikes didn’t have gears, just a single medium gear, which you couldn’t race with, and we got off and pushed them on strong uphill slopes. The gears (4-speeds) were only a privilege of older children, whose legs were long enough for the 28-inch bike.
If I were a child today, I could easily wish for a 7-speed hub gearbox for Christmas, or even a 24-speed one with sprockets to change the gear ratio.
Why would I want such a thing? Let’s see what kind of hill I can go up on and how fast I can ride with a bike, and what these values depend on!
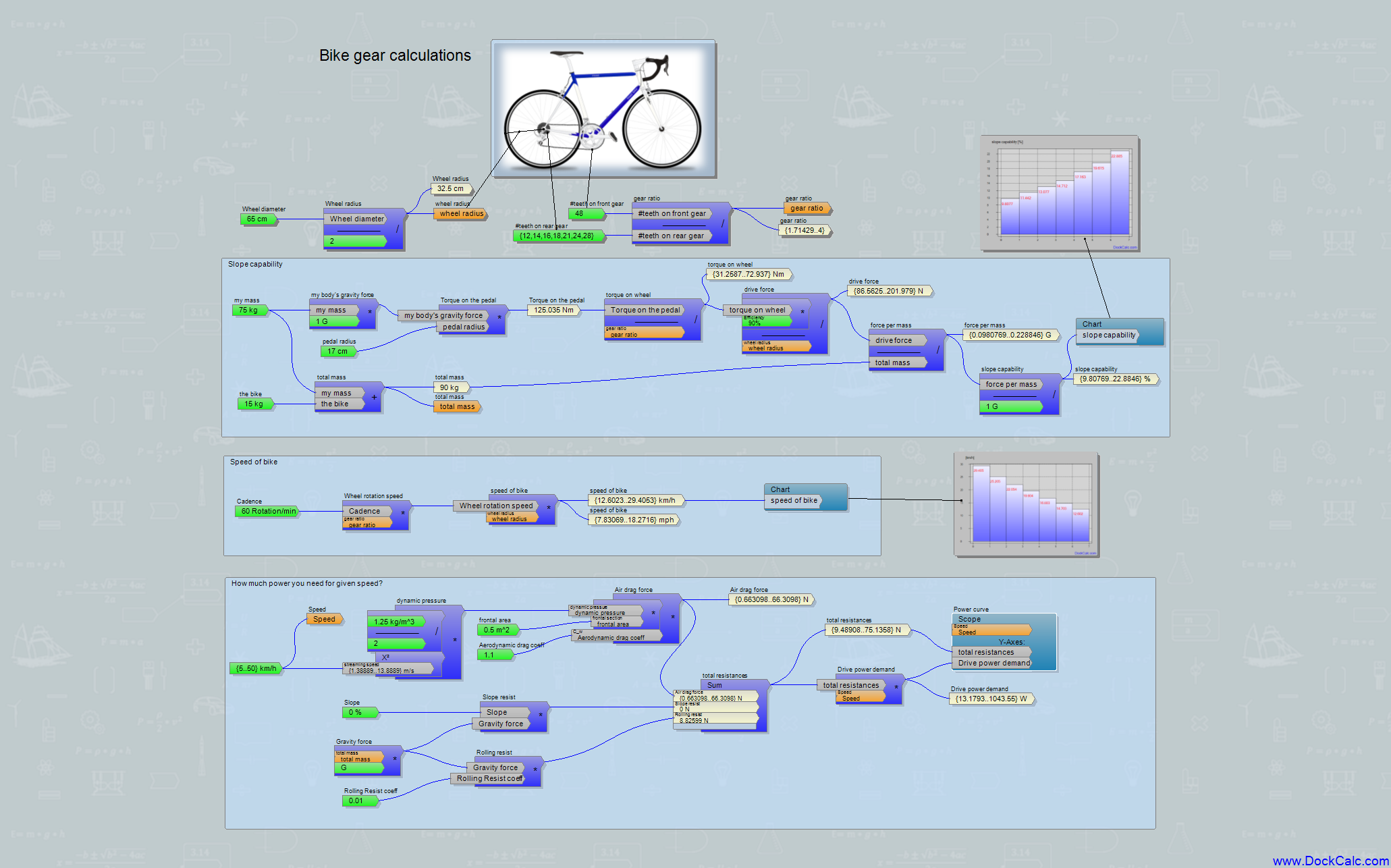
With the DockCalc program, I put a small calculation together for a bicycle, which consists of three parts:
- What uphill slope can I go if I stand on the pedal with my full body weight?
- How fast can I go at a given pedal rotation speed (cadence)?
- What power do I need to exert in order to be able to maintain a given speed?
It is worth looking at the three calculations separately at first, so as not to scare you away. The calculation of the climb that can be overcome (above block) is based on the basic idea that the total weight of the cyclist creates a specific torque on the pedal arm (some “Newton meters or [Nm]”), which will be smaller due to the typical acceleration ratio of the chain drive, and then it can be converted into driving force by dividing it by the radius of the wheel. As this driving force is related to my weight force measured together with the bike, it shows how much of an incline I can still go up (here I only took the forces into account, whether I can handle it by power is another question, and I will come back to it later).
Those who have paid close attention in math class may have noticed that I am neglecting the distorting effect of certain trigonometric functions here for the sake of simplicity, but on those climbs that we are happy to conquer with a bicycle, these distortions do not matter much.
In my simple example, the gears of a bike with a 7-speed chain drive resulted in gradients of roughly 9..22%. For this, of course, you have to get up from the saddle.
The second calculation is about what speed the bike would reach at a given pedaling speed (at given revolutions per minute on the pedals). Here, it may be noticed that the greater the number of teeth of the sprocket on the pedal side compared to the number of teeth on the wheel side (the ratio of the two numbers of teeth is the gear ratio), the faster the bicycle can travel. Obviously, all of this is also proportional to the pedaling speed. For pedaling at 60 revolutions/minute, I got roughly 12 to 29 km/h, depending on which gear I chose. Fortunately, DockCalc calculates this for all 7 gears at once and can display it, for example, in a bar chart.
The third calculation block is for advanced readers, but it can be interesting for everyone: this is the calculation of the power demand. Here we are looking for the answer to how much power (literally, how many Watts) our muscles need to exert in order to overcome the bicycle’s resistance. If there is no uphill, then air drag will be our biggest enemy (it’s easy to see when cycling against the wind). It’s an interesting joke of nature that the air that causes drag is the same air that we gasp for when we turn the pedal really fast. The force of air resistance is proportional to the following factors:
- the frontal area of the cyclist’s silhouette (that’s why it’s worth leaning to the handlebar if you want to go fast),
- the air density (approximately 1.25 [kg/m3] at a pleasant spring temperature)
- the cyclist’s air resistance form factor (bad news: traditional bicycles and their riders produce a catastrophic value of around 1.1, the same figure for a nice streamlined car is around 0.22)
- and finally, the “killer” factor: the square of the speed
If we multiply everything here, we get the force of air resistance, but we need to know the power. High school students still remember: Power=Force*Speed, so for getting power, the above value must be multiplied once more by speed, this is already speed on the power of three ☹. Why does it hurt so much? If you want to reach double speed, your body has to exert 2*2*2=8 times as much power to overcome air resistance. For the human body, power means heavy breathing and high heart rates. Bodies raised on chips and Netflix already suffer from 100W, IronMen athletes produce more than 400 Watts (!!!) permanently for hours.
A stress ECG test gives a good indication of your personal performance. I can tell you that I didn’t overload the equipment either 😊, already at 200 Watts I was really looking forward to getting off the ergometer quickly.
But there is someone well known we do not see racing on a bicycle: Darth Vader. Fate dealt him a doubly bad hand: due to his cloak, he has a lot of air resistance, and he is well known that his lungs don’t perform well either.
When calculating power, the elevation of the road cannot be neglected either, which is proportional to body weight and slope, but luckily, we only have to multiply it once by speed.
The rolling resistance of the wheels is also included in the formula, which can be compared to an incline of less than 1% in the case of a normally inflated tires.
Since this short article is not written as a PhD thesis, I will not include the exact formulas, the DockCalc calculation should be sufficient. If you want to calculate with your own data, feel free to download the DockCalc program and the corresponding calculation here:
You can change the input data in the green blocks by double-clicking.
And since spring is coming soon: let’s experience the calculations in practice on a real bike, it’s much healthier and more exciting!
PS: I am clearly a marketing talent when I say: “don’t bother with my software-product, go for a bike ride instead!” 😊