Background
About physical units
When you hear a physical value like the speed of light or the fronta area of your car or even the height of your own body, the given value expresses a property or a state of something (or somebody).
A physical value consists of a number and a measurement unit:
- 6 feet (the height of a person)
- 20 miles per hour (the speed of a car)
- 2.5 gallons (the fuel in your car)
Actually, the physical value is the multiplication of the pure number and the belonging measurement unit. The measurement unit is a physical value too, having its own pure multiplication number and a measurement unit. There are some standardized base measurement units (Wikipedia: SI Base units) which are agreed internationally as ancestor of other derived units.
| Symbol | Name | Quantity |
| s | second | time |
| m | metre | length |
| kg | kilogram | mass |
| A | ampere | electric current |
| K | kelvin | thermodynamic temperature |
| mol | mole | amount of substance |
| cd | candela | luminous intensity |
Derived units and any physical value can be expressed using these base units by multiplying/dividing with each other and with pure numbers.
Example:
The base unit of length is the meter [m]. Distance is the dimension (the art of physical value), its internationally agreed base unit is the well-known meter.
If I multiply length by length, I get a surface or area as art of the physical value. The measurement unit is accordingly [m*m] = [m^2] “square meter”. I can measure surfaces, cross sections, areas with this measurement unit.
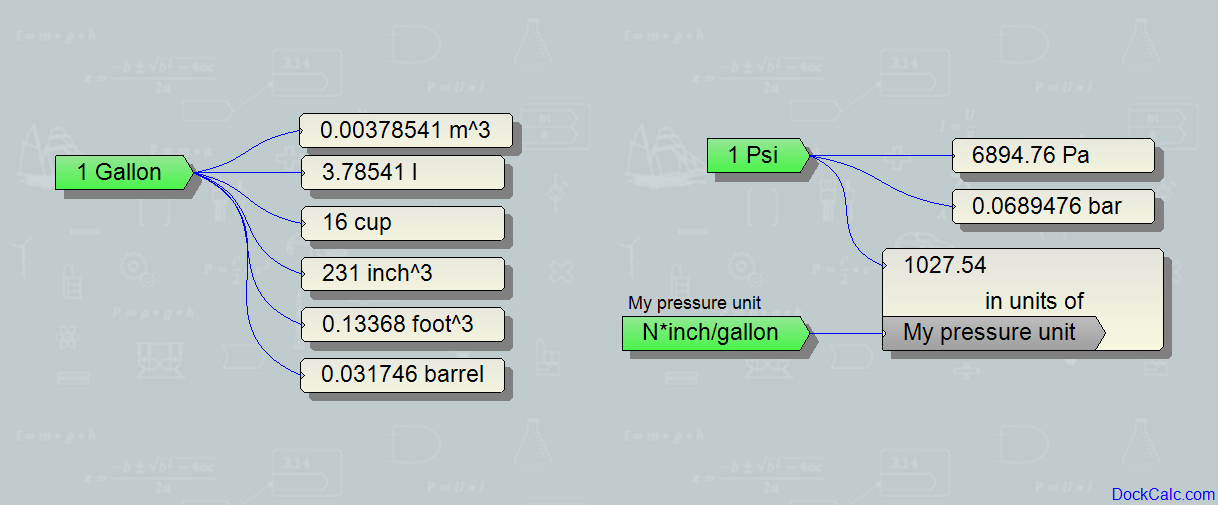
When I multiply length by length and again by length, I get volume. Accordingly, the measurement unit for volume is [m*m*m] = [m3] “cubic meter”. Although cubic meter is sometimes used in our daily life, it is more common to use “liter” (0.001 m3) or gallon (0.00378541 m3) instead, just because these are closer to our daily consumptions of drinks. Gallon, liter, m3 and several other volume units (like “cubic light year” ?) can be translated into each other because they all express the same kind of physical meaning: volume (which is the 3rd power of a length).
When I say “2.5 gallon equals 0.00946353 m3“ I mean (as an engineer):
“if I multiply the number 2.5 with the meaning of gallon I get the same physical volume as when I would multiply the number 0.00946353 with the meaning of meter 3 times after each other” (to get to the 3rd power of meter).
On the other hand, you cannot simply convert gallon into hours because they belong to different dimensions (volume vs time). The question “how many gallons is one hour?” makes not much sense because they are not compatible, you cannot give any well-defined answer.
Luckily, you are allowed to “play” with measurement units as far as you multiply or divide them with each other. Having some luck, you can find a meaning to the resulting derived dimensions and belonging measurement units.
Let us see some examples:
- Length divided by time is speed (m/s, miles per hour,…)
- Length divided by time and again divided by time is acceleration (m/s2 or our famous G-force /9.80665 m/s2/)
- Acceleration (which itself is length/time2) multiplied with mass results force (we in Europe like to measure it in Newtons [kg*m/s2])
Playing further: when I divide force with the square of length (which is area or surface) I get pressure. Pressure is finally mass divided by length divided by square of time. Depending on where you live you might use the unit of Pascal [kg/m/s2] or Bar [100000 Pascal] or Psi (“pounds per square inch” = 6894.76 Pascal).
Now you might feel tired. No worry, DockCalc is made for you: it takes over the hurdle of all those conversions, so you can concentrate on your core topic.
Have Fun with DockCalc!