Fahrrad-Übersetzungen und Luftwiderstand berechnen
Eine der genialsten Erfindungen der Menschheit ist das Fahrrad. Es nutzt die Muskelkraft des Menschen sehr effizient, um sich fortzubewegen, es viel schneller als das Laufen, gesund und es kann sogar eine Last auf dem Gepäckträger tragen. Ich kann es kaum erwarten, in der Frühlingssonne Fahrrad zu fahren. Diese Leidenschaft geht auf meine Kindheit zurück, als ich viel Fahrrad gefahren bin und als technisch interessiertes Kind immer über eine technische Modifikation nachgedacht habe. Einmal haben wir das Hinterrad meines Fahrrads durch ein viel kleineres Rad eines Kinderfahrrads ersetzt und uns darüber gefreut, wie leicht es aufgrund der geänderten Übersetzung möglich war, bergauf zu fahren. Wie schön wäre es gewesen, wenn ich das Hinterrad für die aktuelle Straße hätte wählen können. Dieser Wunsch wurde mir später durch die Gangschaltung erfüllt. Ja, Kinder von heute, damals (ich rede von der Zeit um etwa 1980) hatten Kinderfahrräder keine Gangschaltung, sondern eine mittlere Übersetzung, mit dem man nicht rasen konnte, und wir mussten an starken Anstiegen abgestiegen und schieben. Das Getriebe (4-Gang) war wohl nur das Privileg älterer, deren Beine schon lang genug waren um 28-Zoll-Bike zu fahren.
Wenn ich heute ein Kind wäre, könnte ich mir zu Weihnachten leicht eine 7-Gang-Nabenschaltung wünschen oder sogar ein 24-Gang-Rad, mit Kettenschaltung.
Warum sollte ich so etwas wollen? Mal sehen, welche Art von Hügel ich hochfahren kann und wie schnell ich mit einem Fahrrad fahren kann und wovon diese Werte abhängen:
Mit dem Programm DockCalc habe ich für ein beliebiges Fahrrad eine kleine Berechnung zusammengestellt, die aus drei Teilen besteht:
- Welche Steigungen kann ich bewältigen, wenn ich mit vollem Körpergewicht auf dem Pedal stehe?
- Wie schnell kann ich bei einer bestimmten Pedalumdrehungsgeschwindigkeit (Kadenz) fahren?
- Welche Leistung muss ich aufbringen, um eine bestimmte Geschwindigkeit halten zu können?
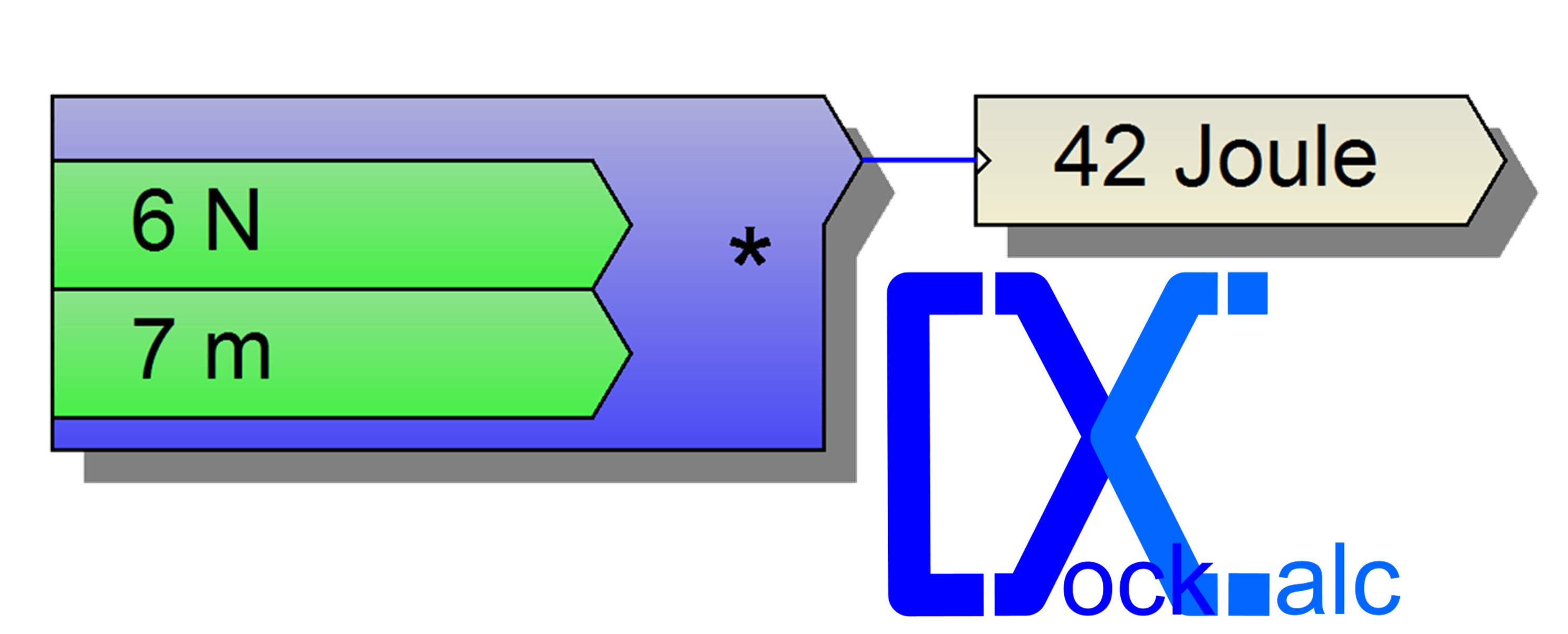
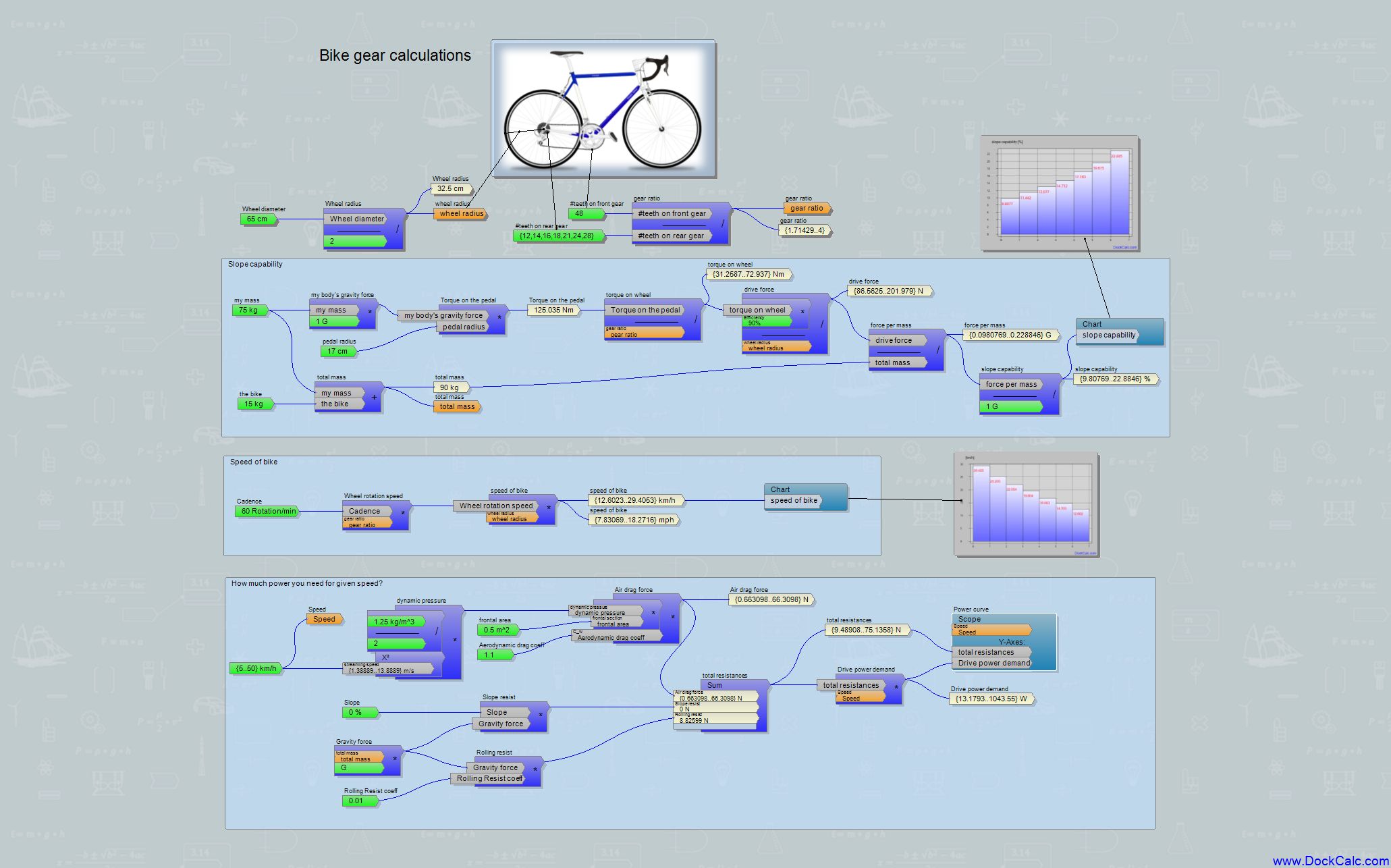
Es lohnt sich, die drei Berechnungen zunächst getrennt zu betrachten, um Sie nicht abzuschrecken. Die Berechnung des zu bewältigenden Anstiegs (oberhalb der Abbildung) basiert auf der Grundidee, dass das Gesamtgewicht des Radfahrers ein bestimmtes Drehmoment am Pedalhebel erzeugt (einige „Newtonmeter [Nm]“), das aufgrund der typischen Übersetzung des Kettenantriebs verkleinert wird und kann dann in Antriebskraft umgewandelt wird, indem sie durch den Radius des Rads geteilt wird. Da diese Antriebskraft in Relation zu meiner mit dem Rad gemessenen Gesamtgewichtskraft steht, zeigt sie an, wie viel Prozent Steigung ich noch hochfahren kann (hier habe ich nur die Kräfte berücksichtigt, ob bei mir die Puste ausgeht, ist eine andere Frage, und das werde ich später ansprechen).
Wer im Matheunterricht genau aufgepasst hat, dem ist vielleicht aufgefallen, dass ich hier der Einfachheit halber die verzerrende Wirkung bestimmter trigonometrischer Funktionen vernachlässige, aber an jenen Steigungen, die wir gerne mit dem Fahrrad bezwingen, fallen diese Verzerrungen kaum ins Gewicht.
In meinem einfachen Beispiel ergibt die Schaltung eines Fahrrads mit 7-Gang-Kettenschaltung Steigungen von ca. 9..22%. Dafür muss man natürlich aus dem Sattel aufstehen.
Bei der zweiten Berechnung geht es darum, welche Geschwindigkeit das Fahrrad bei einer bestimmten Tretgeschwindigkeit (wie viele Umdrehungen pro Minute auf den Pedalen) erreichen würde. Hierbei ist zu beachten, dass das Fahrrad umso schneller ist, je größer die Zahnzahl des Kettenrades auf der Pedalseite im Vergleich zur Zahnzahl des Kettenrades auf dem Laufrad ist (das Verhältnis der beiden Zahnzahlen ist die Übersetzung). All dies ist natürlich auch proportional zur Tretgeschwindigkeit. Beim Treten mit 60 Umdrehungen/Minute komme ich auf etwa 12 bzw. 29 km/h, je nachdem welchen Gang ich wähle. Glücklicherweise berechnet DockCalc dies für alle 7 Gänge auf einmal und kann es beispielsweise in einem Balkendiagramm anzeigen.
Der dritte Berechnungsblock ist etwas für Fortgeschrittene, kann aber für jeden lehrreich sein: Das ist die Berechnung des Leistungsbedarfs. Hier suchen wir nach der Antwort darauf, wie viel Kraft (wörtlich: wie viele Watt) unsere Muskeln aufbringen müssen, um den Widerstand des Fahrrads zu überwinden. Wenn es nicht bergauf geht, ist der Luftwiderstand unser größter Feind (gut zu erkennen, wenn man gegen den Wind fährt). Es ist ein interessanter Witz der Natur, dass die gleiche Luft, die den Luftwiderstand verursacht, die gleiche Luft ist, wonach wir schnappen, wenn wir das Pedal sehr schnell treten. Die Kraft des Luftwiderstands ist proportional zu den folgenden Faktoren:
- mit der frontalen Oberfläche der Silhouette des Radfahrers (daher lohnt es sich zu beugen, wenn es schnell gehen soll),
- mit der Luftdichte (ca. 1,25 [kg/m3] bei angenehmer Frühlingstemperatur)
- mit dem Luftwiderstands-Formfaktor des Fahrradfahrers (schlechte Nachrichten: herkömmliche Fahrräder und ihre Fahrer zusammen produzieren einen katastrophalen Wert von etwa 1,1. Der gleiche Wert für ein schönes windschnittiges Auto liegt bei etwa 0,22)
- und schließlich der „Killer“-Faktor: das Quadrat der Geschwindigkeit
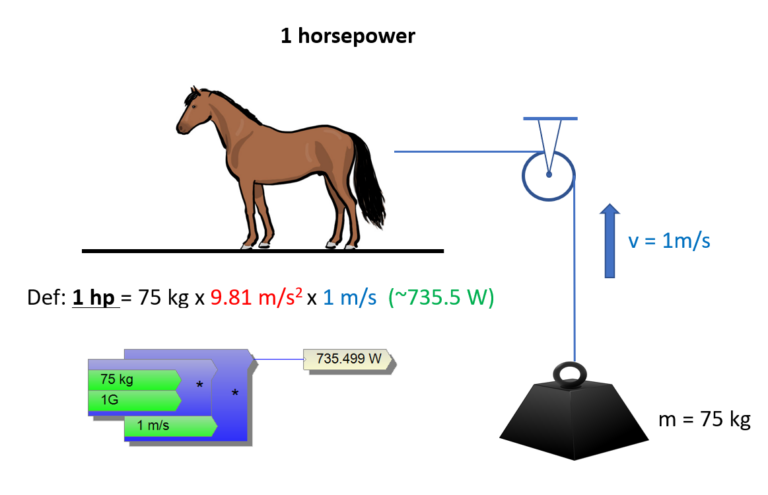
Wenn wir hier alles multiplizieren, erhalten wir die Kraft des Luftwiderstands. Gymnasiasten erinnern sich noch: Leistung=Kraft * Geschwindigkeit, also für Leistung muss der obige Wert noch einmal mit Geschwindigkeit multipliziert werden, das ist schon die dritte Potenz ☹. Warum tut es so weh? Willst du die doppelte Geschwindigkeit erreichen, muss dein Körper 2*2*2=8 Mal so viel Leistung abgeben, um den Luftwiderstand zu überwinden.
Für den Körper bedeutet Leistung Hecheln und Herzklopfen. Auf Chips und Netflix aufgezogene Körper leiden schon bei 100W, IronMan geben mehr als 400 Watt (!!!) dauerhaft ab.
Ein Belastungs-EKG-Test gibt einen guten Hinweis auf deine Leistungsfähigkeit. Ich kann euch verraten, dass ich das Gerät auch nicht überlastet habe, bei 200 Watt habe ich mich richtig darauf gefreut, vom Ergometer abzusteigen 😊.
Aber wir sehen eine bestimmte Berühmtheit selten auf einem Fahrrad rasen: Darth Vader. Das Schicksal hat ihm doppelt übel getroffen: Durch seinen Umhang hat er Luftwiderstand ohne Ende, und seine Lungen können bekanntlich auch nicht gut mit der Belastung umgehen.
Bei der Berechnung der Leistung darf auch die Steigung der Straße nicht vernachlässigt werden, die proportional zu Körpergewicht und Steigung ist, aber zum Glück nur einmal mit der Geschwindigkeit multipliziert werden muss.
Auch der Rollwiderstand der Laufräder fließt in die Formel ein, was bei normal aufgepumpten Reifen mit einer Steigung von weniger als 1 % vergleichbar ist.
Da dieser kurze Artikel nicht für eine Doktorarbeit geschrieben wird, werde ich die Formeln nicht mitgeben, lieber die DockCalc-Berechnung sollte hier als Bild stehen. Wenn du mit deinen eigenen Daten rechnen möchtest, kannst du das Programm DockCalc und die obige Berechnung herunterladen:
Du kannst die Eingangsdaten in den grünen Blöcken ändern (per Doppelklick).
Und da bald der Frühling kommt: Lasst uns das Rechnen in der Praxis erleben, es ist viel gesünder und interessanter so!
PS: So sieht eine perfekte Werbung aus: “Kümmere dich nicht um mein Programm, mach stattdessen eine Radtour!” 😊