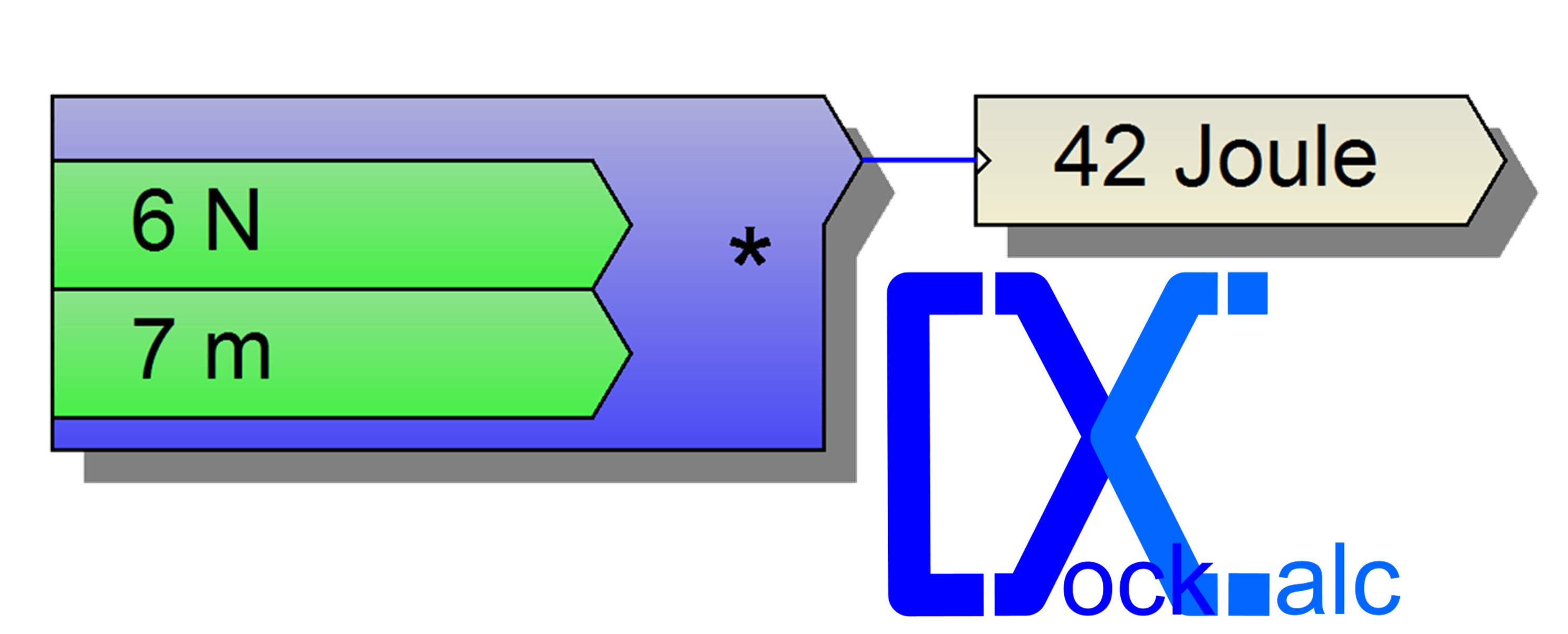
Die Fläche von Puderzucker

Je näher Weihnachten rückt, desto mehr köstliche Plätzchenrezepte erscheinen und die Häuser sind erfüllt vom Duft festlicher Kekse. Natürlich darf auf den Plätzchen auch eine dünne Puderzuckerschicht nicht fehlen, die vielleicht ein bisschen die verschneite Winterlandschaft symbolisiert. Wenn wir es essen, schmilzt es fast in unserem Mund, im Gegensatz zu großem Kristallzucker, der beim Kauen zwischen unseren Zähnen knirscht. Aber warum ist Puderzucker so lecker, was ist das Geheimnis, das dem Kristallzucker fehlt? Wenn ich es als Ingenieur betrachte, dann ist meine Vorstellung, dass man es nicht mehr kauen muss, weil es schon feinkörnig ist und eine große Oberfläche hat, also schnell auflöst. Wenn ich Puderzucker in meinen Tee gebe, löst er sich viel schneller auf als Kristallzucker. Und wenn ich in einem Hotel zufällig nur Zucker in Form von großen Körnern finde, muss ich eine Viertelstunde warten, bis er verschwunden ist und ich endlich meinen Tee trinken kann. Wenn also die Oberfläche so wichtig ist, wie groß ist eigentlich die Oberfläche von Puderzucker? Mit einem Gedankenexperiment können Sie sehen, dass je kleiner das Korn ist, desto mehr Oberfläche entsteht:

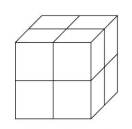
Denken Sie darüber nach, wenn wir ein einzelnes Zuckerkristall hätten, der so groß wie ein Rubik-Würfel wäre, wäre nur seine äußere Oberfläche freigelegt, und jedes Getränk, das wir süßen wollten, könnte nur darauf zugreifen. Es würde eine ganze Weile dauern, bis es sich auflöst. Wenn ich den großen Würfel teilen würde, indem ich ihn in alle 3 Richtungen halbiere, würde ich insgesamt 8 Hälften des Würfels erhalten. Beide Seiten der Schnittebenen würden als neue Außenfläche freigelegt. Wenn die Kante des ursprünglichen Würfels “a” war, dann habe ich 3 neue Schnittebenen (eine horizontal und zwei senkrecht zueinander vertikal), entlang denen ich 3*2 Stücke “a*a”-Fläche erhalten habe. Ein Multiplikator von 2 deutet darauf hin, dass beide Seiten der Schnittebene zählen. Wenn die Vorstellungskraft von jemandem auch praktische Erfahrung erfordert, empfehle ich, die Übung beispielsweise mit Käse durchzuführen.

Wenn die Kante des ursprünglichen Würfels “a” war, dann ist seine Oberfläche 6*a². Durch die Teilung kam eine Fläche von 3*2*a² hinzu, was bedeutet, dass ich die Fläche des Würfels verdoppelt habe. Das sieht man auch daran, dass die Gesamtfläche der 8 Würfel mit der Kantenlänge a/2 ist: 8(Stück)*(a/2)²*6 = 8*a²/4*6 = 12*a².

Wenn ich die kleineren Würfel noch einmal auf die gleiche Weise entlang 3 Ebenen halbiere, entstehen wieder neue Flächen.

Wenn ich also einen Würfel in 8 kleinere Würfel schneide, indem ich die Seiten halbiere, verdoppelt sich seine Oberfläche. Wenn ich das Zerteilen einer Mühle überlasse und aus einem größeren Block viele winzige Würfel (Zuckerkörner) mache, wird die Gesamtfläche umso größer, je kleiner ich mahle. Dabei stellt sich die Frage:

Wie viel Oberfläche hat eigentlich eine 500-g-Packung Puderzucker insgesamt?

Wenn ich ein böser Mathelehrer wäre, würde ich manuell mit den Schülern zählen lassen, wie viele Flächen man erhält, wenn man, sagen wir, 10-15-mal nacheinander dividiert. Anstelle eines schlechten Mathelehrers bin ich eher ein fauler Ingenieur, daher arbeite ich mit folgendem Gedankengang:

1: Ich schreibe das Verhältnis von Oberfläche und Volumen eines Würfels gegebener Größe „a“ auf: Oberfläche=6*a², Volumen=a3. Fläche/Volumen=6*a²/a3=6/a. Die Division durch „a“ zeigt unsere Vermutung: Je kleiner „a“ (Korngröße), desto größer ist das Verhältnis zugunsten der Fläche und das Verhältnis hat sogar eine Einheit: [1/m]. Ich habe im Internet typische Werte zwischen 0,02mm und 0,1 für die Größe “a” beim Puderzucker gefunden.

2: Ich berechne das Volumen eines 500g Zuckerblocks (man braucht nur die Dichte des Zuckers: laut unzähligen Quellen sind es ca. 1600 kg/m³). 0,5 kg/(1600 kg/m³) = 0,0003125 m³ (dh 0,3125 Liter).

3: Mit den beiden obigen Daten kann ich die Gesamtoberfläche der gesamten Zuckerschachtel für eine beliebige “a” -Körnung berechnen:

Gesamtoberfläche = Volumen * (Oberflächen-Volumen-Verhältnis). 500g Puderzucker entsprechen bei mir in etwa der Grundfläche einer Wohnung (75m²).

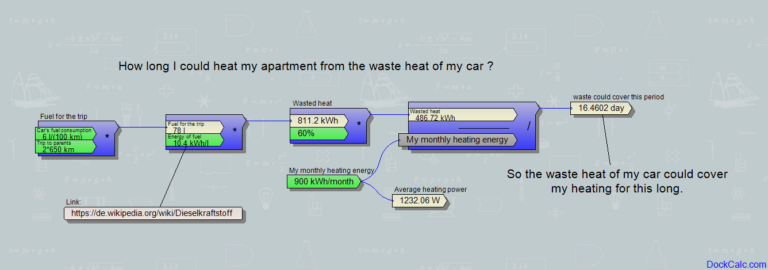
Ich habe eine solche Berechnung mit dem Programm DockCalc erstellt, damit ich schnell Ergebnisse für alle möglichen Datenkombinationen erhalten kann:

Übrigens, das Effekt (Fläche zu Volumen hängt von Größe ab) ist in unzähligen Bereichen zu erleben, hier einige Beispiele:

• Große Regentropfen fallen schneller als feinkörniger Regen (sie werden durch ihre Oberfläche gebremst aber proportional ihres Volumens /ihr Gewicht/ angetrieben). Sind die Tröpfchen klein genug (z. B. Nebel, Wolken), fallen sie so langsam, dass selbst der kleinste Aufwärtszug sie stoppt oder sogar anhebt.
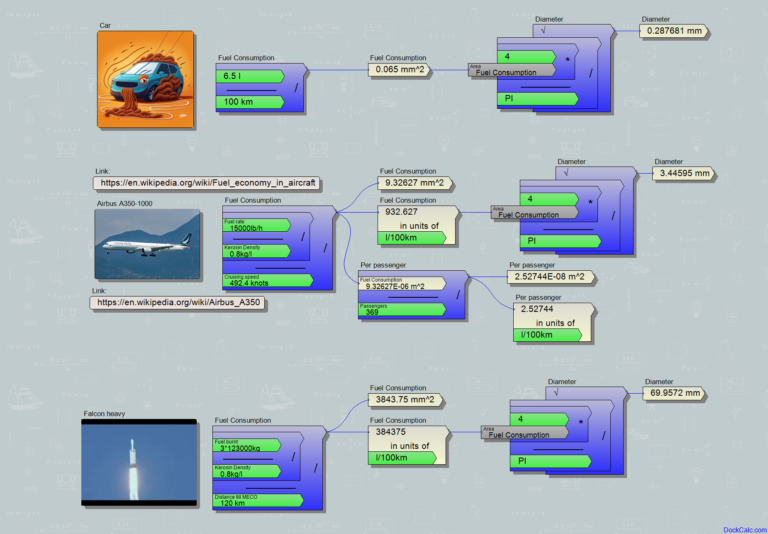
• In Motoren ist eine große Oberfläche für die Kraftstoffverbrennung wichtig, daher versuchen Ingenieure, den Kraftstoff in möglichst kleine Tröpfchen zu zerstäuben. Früher der Vergaser (Link), (von Maybach, Bánki-Csonka), heute die Einspritzsysteme lösen diese Aufgabe. Um die Tröpfchen-größe zu minimieren, versucht man den Einspritzdruck in Dieselmotoren (über das 2000-fache des atmosphärischen Drucks) zu erhöhen, damit der Sprit auf die kleinste Partikelgröße zerstäubt wird. Je besser das gelingt, desto mehr Sauerstoff kann bei der Verbrennung an die Tröpfchen gelangen und desto weniger schädlicher Ruß entsteht.
• Das Körpergewicht von Lebewesen ist proportional zur 3. Potenz ihrer Größe, aber der Querschnitt ihrer Knochen und Muskeln ist nur proportional zum Quadrat ihrer Größe. Je größer ein Organismus ist, desto größer ist die Belastung seiner Knochen und Muskeln. Es könnte Dinosaurier mit so großen Körpern gegeben haben, von denen Wissenschaftler glauben, dass sie normalerweise nur im Wasser existieren könnten, weil ihre Beine ihr Gewicht an Land nicht hätten tragen können. Kleinere Tiere und Insekten hingegen überstehen Stürze aus großer Höhe schadlos. Der Grund ist Teils der Luftwiderstand, teils die spezifische Belastung der Beine, entscheidend ist bei beiden das Verhältnis von Oberfläche und Volumen.

Naja, zurück zu den Kuchen: Guten Appetit und Vorsicht mit Puderzucker: Schon ein Quadratmeter macht dick 😊!