Wie frei ist ein freies Elektron?

Heute ist Freitag. Man ist ab heute Abend frei von der Arbeit, ab ins Wochenende! Freiheit ist etwas, wofür sich lohnt zu kämpfen, Freiheit ist das Wort, das entlang der Geschichte immer groß geschrieben wird. Auf diese Weise können wir jeden beneiden, der frei ist, obwohl beim „Freimaurer“ bin ich nicht sicher, ob alle Maurer sich als frei betrachten. Jedenfalls wenn jemand frei ist, kann er alles tun, gehen, wohin er/sie will.

Dies kann beispielsweise für ein freies Elektron gelten -oder doch nicht? Sind freie Elektronen wirklich frei?

Die sind nämlich jene Elektronen, die zum Beispiel in einem metallischen Gitter schon bei kleinsten elektrischen Feldstärken beliebig wandern können, da sie keinem Atomkern zugeordnet und gebunden sind. Wenn das nicht ausreichend beneidenswert ist, werfen wir einen Blick auf unsere neueste Stromrechnung und sehen, dass Elektronen sehr gut bezahlt sind.

Irgendwie sind Elektronen doch negativ eingestellt. Aber was hätten die zu meckern?

Ich habe ein wenig recherchiert, und überlegt wie weit die reisen können, wenn die Lust auf ein Abenteuer haben. In der Schule lernen wir, dass sich elektrische Energie mit Lichtgeschwindigkeit entlang dem Draht bewegt. Wenn ich an eine Ender einer langen Leitung in Budapest einen Schalter einschalte, die andere Ende z. B. an meinem Lieblingsstrand an der Adria mit einer Lampe verbinde, dann nach ca. 2 Millisekunden, also zwei Tausendstelsekunden, fließt dort Strom, die Lampe leuchtet. Wenn das keine Freiheit ist, dann nichts, denn ich bewältige die gleiche Strecke im besten Fall in 6 Stunden Autofahrt.

Aber lasst uns einen Moment überlegen! Niemand hat gesagt, dass das Elektron vom Schalter in Budapest „höchstpersönlich“ in einem Augenblick mit Lichtgeschwindigkeit das andere Ende des Drahtes beispielsweise in Rovinj erreichen würde. Nein, die elektrische Wechselwirkung zwischen den Elektronen, quasi der Effekt der Abstoßung, wird schnell übertragen, aber nicht das Elektron selbst. Das arme Elektron bleibt fast an der Stelle nur seine Energie wird entlang den Draht weitergeleitet.

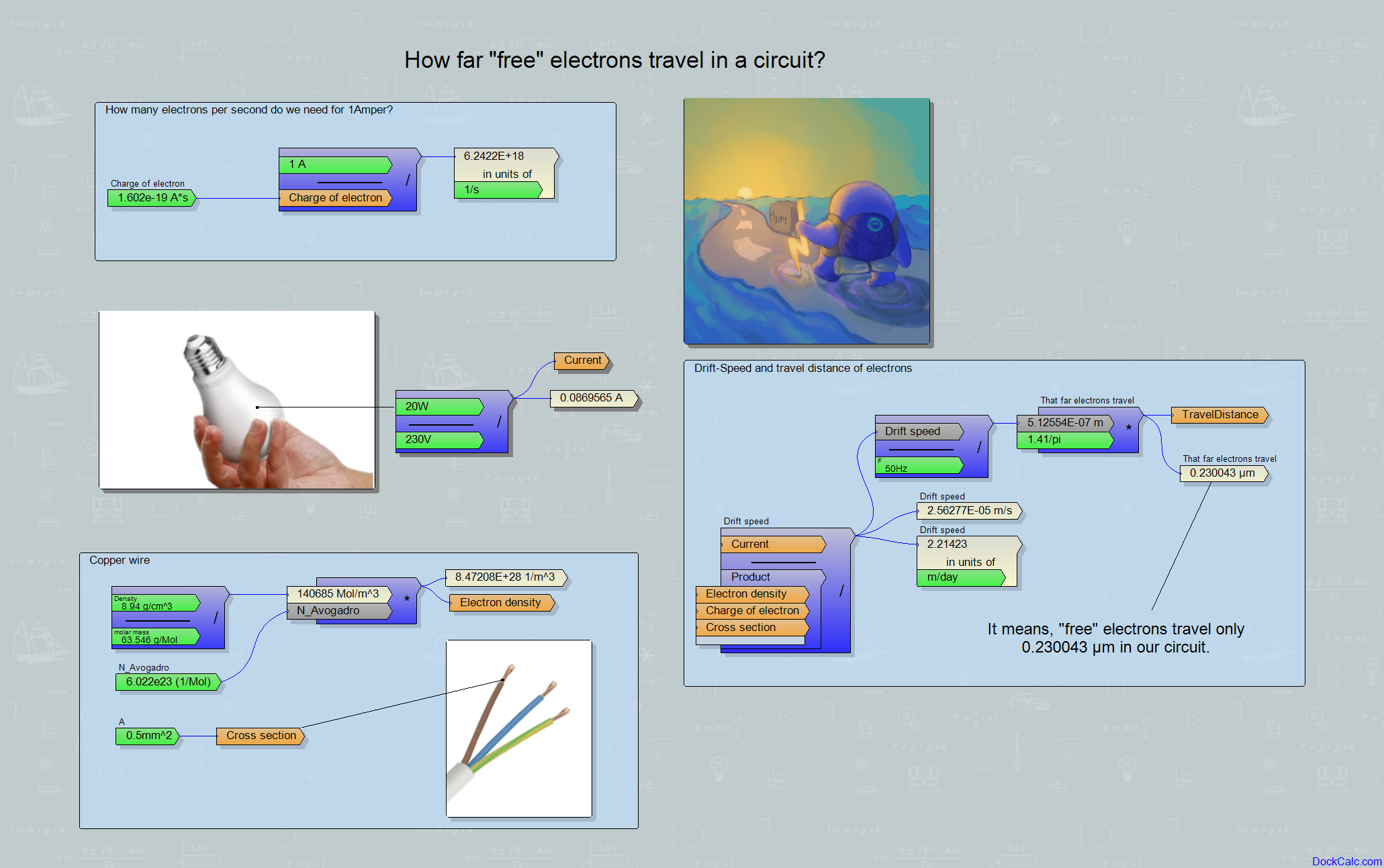
Aber so etwas lässt sich berechnen, denn wir haben gelernt, dass eine Coulomb-Ladung bei einem Strom von einem Ampere in einer Sekunde einen gegebenen Querschnitt durchläuft. Wir müssen nur wissen, wie dicht die Elektronen im Draht sind, und dann können wir herausfinden, wie weit sie sich bewegen müssen und wie schnell sie sich bei einem bestimmten Strom bewegen. Wikipedia sagt, dass ein Elektron eine Ladung von −1,602*10⁻¹⁹ Coulomb hat. Ein Ampere bedeutet also, dass ungefähr 6,2422 * 10¹⁸ Elektronen irgendwo in einer Sekunde passieren. Natürlich müssen sie dafür umso schneller gehen, je dünner der Draht ist, aber wenn der Draht zu dünn ist, erwärmt er sich aufgrund des Widerstands, also wir nicht unendlich viel Strom durch einen dünnen Draht schicken können. Ich muss hier anmerken, dass das Alltagsleben eines Elektrons nur stark vereinfacht so aussieht und noch dazu können sie nicht mit bloßem Auge (auch nicht mit einem Mikroskop) beobachtet werden.  Diejenigen, die Elektronen in ihren Händen gespürt haben, haben zwar eine bleibende Erinnerung gewonnen, die zu verstehen tun sie immer noch nicht.

Gegenstand meiner Überlegungen hier und jetzt ist nur die mittlere Geschwindigkeit von Elektronen in einem Leiter, die sogenannte Driftgeschwindigkeit, die ich im Folgenden berechnen möchte. Wir haben gerade eingesehen, wie viele Elektronen ein bestimmter Strom pro Sekunde bedeutet, und wenn wir wüssten, wie dicht die Elektronen den Leiter „bewohnen“, dann lässt sich daraus einfach ihre Geschwindigkeit berechnen:

Driftgeschwindigkeit = Strom / (Elektronendichte * Elektronenladung * Drahtquerschnitt)

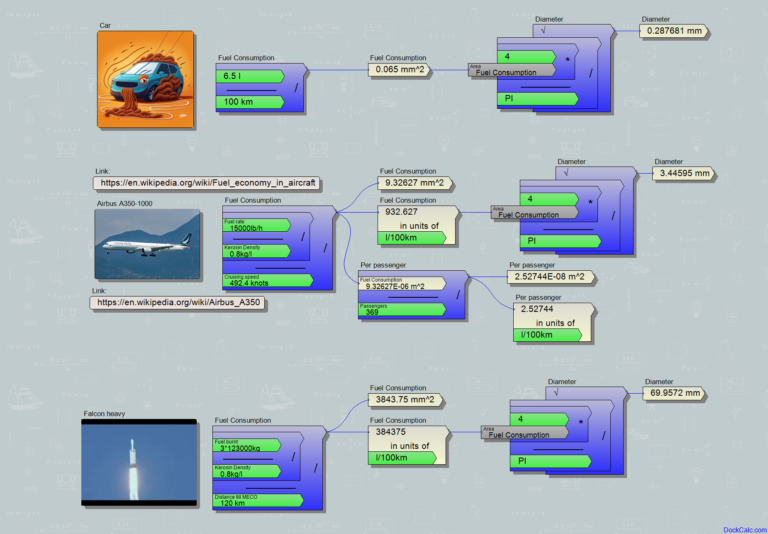
Die Elektronendichte kann etwas Kopfzerbrechen bereiten, aber wenn wir mit Kupfer rechnen (die Drähte bestehen oft daraus), dann erhalten wir durch die Kombination von Materialtabelle und Chemieunterricht Daten wie die Dichte von Kupfer (8,94 g/cm³), seine Molmasse (63,546 g/Mol), die in einen Wert von 140685 Mol/m³ umgerechnet werden, was, multipliziert mit der Avogadro-Zahl (6,022*10²³),  8,5*10²⁸ Atome/m³ ergibt, also die Zahl, wie viele Atome in einem Kubikmeter Kupfer sind. Kupfer hat ein freies Elektron pro Atom (jedes Atom opfert jeweils ein Elektron für die Gemeinschaft), daher beträgt die Dichte der freien Elektronen genau 8,5 * 10²⁸ Elektronen pro Kubikmeter. An den 28 Nullen ist zu spüren, dass so viele Elektronen schon mit sehr geringen Geschwindigkeiten eine erhebliche Stromstärke darstellen. Schauen wir uns ein praktisches Beispiel an: Eine 20-Watt-LED-Lampe, die mit Netzspannung (230 V) betrieben wird, verbraucht nur 0,087 A Strom. Die üblichen Leitungsquerschnitte im Haushalt liegen bei etwa 0.5 mm² und 1.5 mm², wählen wir einen dünnen, damit unsere Elektronen etwas weiter reisen können: 0.5 mm²!

Setzt man alles in die oben geschriebene Formel ein, ergibt sich die Driftgeschwindigkeit wie folgt:

Driftgeschwindigkeit = 0.087 A/(8.5*10²⁸ Elektronen/m³*1.602*10^-19 Coulomb*0.5 mm²) = 2.563*10^-5 m/s

das heißt, nicht mehr als 2.215 Meter pro Tag (!).

Und erst jetzt kommt die wirklich enttäuschende Tatsache:

wir betreiben unsere Maschinen und Lichter mit Wechselstrom.  Daher bewegt sich unser Elektron nicht nur mit minimaler Geschwindigkeit, aber das auch schnell hin und her. Die Strecke entlang ein Elektron „wandert“ ist somit auf weniger als ein Mikrometer begrenzt. Natürlich können wir aus reinem Mitgefühl unseren Elektronen zu etwas Abenteuer verhelfen, wenn wir dünnere Drähte und leistungsfähigere Maschinen verwenden, so dass wir den Lebensraum unserer negativen Freunde sogar auf einige Millimeter vergrößern, obwohl Sicherheits- und Sparüberlegungen so etwas nicht empfehlen. Trösten wir uns damit, dass uns unsere Elektronen wahrscheinlich viele zehn Jahre uns treu zur Seite stehen, uns dienen und es nicht auszuschließen ist, dass die gleichen Elektronen, die gerade Helligkeit für die Abitur-Vorbereitung unseres Kindes anbieten, haben noch die ersten Gehversuche des Kindes miterlebt.

Gehen wir also behutsam mit sie um und lassen einige von ihnen in einer Lichterkette auf den Weihnachtsbaum steigen, damit sie mit uns zusammen das kommende Weihnachtsfest feiern können!

Ich empfehle, die Durchführung der Berechnungen in diesem Artikel zuhause nur für gut ausgebildeten Fachleuten mit starken Nerven oder denen, die die DockCalc Calculator-Software bereits heruntergeladen haben, denn damit wäre alles so einfach: